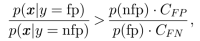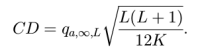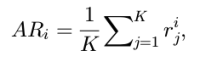Сравнительный анализ моделей классификации для задачи прогнозирования дефектов программного обеспечения: существующие фреймворки и открытия.

Stefan Lessmann, Student Member, IEEE, Bart Baesens, Christophe Mues, and Swantje Pietsch

В данной работе рассматривается прогнозирование дефектов программного обеспечения – задача выявления программных модулей, склонных к ошибкам, с помощью метрики на основе классификации. Было замечено, что большинство сбоев программного обеспечения системы содержатся в небольшом количестве модулей. Следовательно, своевременное выявление этих модулей способствует эффективному распределению ресурсов тестирования и улучшению архитектуры, предлагая более строгий дизайн сегментов высокого риска.

Классификация является популярным подходом для прогнозирования дефектов программного обеспечения и включает категориальные модули, представленные набором метрик: подверженные ошибкам(fp — fault-prone) и не подверженные ошибкам (nfp — non-fault-prone). В решении рассматриваемой задачи были применены различные типы классификаторов, в том числе нейронные сети, статистические методы, tree-based модели и т. д. Однако результаты превосходства одного метода над другим, как и полезность метрической классификации, не аргументированы в различных исследованиях. Однако, прежде чем мы не разработаем надежные исследовательские процедуры, мы не можем быть уверенны в выводах сравнительных исследований моделей прогнозирования программного обеспечения. Причины, по которым выводы вышеупомянутых исследования ставятся под вопрос могут быть следующими. Некоторые исследования полагались на небольшие наборы данных, что, естественно, ограничивает обобщаемость наблюдаемых результатов. Кроме того, в исследованиях использовались различные показатели точности, что приводило к противоречивым результатам, особенно, если они основывались на fp и nfp модулях, что будет рассмотрено далее. Наконец, статистическая проверка гипотез, которая будет предложена в данной работе, не имеет широкого применения в решении рассматриваемой задачи, хотя является стандартной практикой для получения выводов без проверки реальной значимости.

Для решения обозначенной пробшлемы мы предлагаем фреймворк для сравнительной классификации в задаче прогнозирования дефектов программного обеспечения и проводим сравнительный анализ 22 различных моделей классификации над 10 наборами данных из репозитория NASA Metrics Data (MDP). Сравнения проводятся по метрике AUC (area under the receiver operating characteristics curve), как наиболее информативном и объективном показателе точности прогнозирования.

Для начала, обсудим трудности, связанные с оценкой модели классификации в рассматриваемой задаче и введем аннонсированную ранее процедуру статистического тестирования, применяемую в рамках эксперимента сравнительного анализа. Рассмотрим оценки точности, основывающиеся на fp и nfp:

Precision = TP / (TP + FN)

Recall = FP / (TN + FP)

Здесь TP (true positive) – количество модулей, явзяющихся fp, и классифицированных правильно; TN (true negative) – количество nfp модулей, классифицированных корректно; FP (false positive) – количество nfp модулей, классифицированных как fp; FN (false negative) – количество fp модулей, классифицированных как nfp. Мы полагаем, что подобные метрики, хоть и имеют несомненную практическую ценность, концептуально не подходят для эмпирических сравнений конкурентной эффективности алгоритмов классификации, так как построены из дискретной классификации модулей в fp и nfp. Большинство классификаторов не производят четкой классификации, вместо этого определяя вероятности принадлежности классу, и используют пороги, преобразующие непрерывное предсказание (вероятность) в дискретную классификацию. Для определения оптимального порога как правило используется метод Байеса:

где p(fp) и p(nfp) — априорные вероятности; p(y = fp | x) и p(y = nfp | x) — апостериорные вероятности, являющиеся обектом оценивания в задаче классификации; p(x | y = fp) и p(x | y = nfp) — условные вероятности классов из теоремы Байеса; C_FP, C_FN — стоимости FP и FN ошибок соответственно. Таким образом, классификаторы должны быть сравнены не только с запуском на одинаковых данных, но и с использованием одинаковой процедуры определения порога. Однако, стратегии определения порогов не не уточняются в сравнительных исследованиях. Именно по этой причине сравнение алгоритмов с помощью дискретных классификаций не является корректным и приводит к несогласованностям в различных исследованиях.

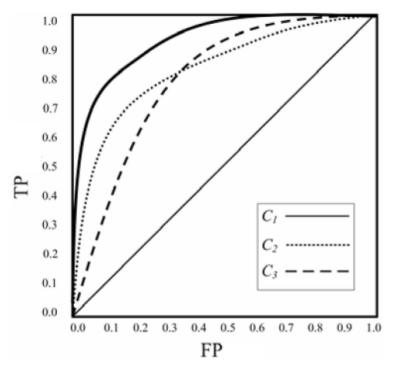
Рис. 1. ROC-кривая. Классификатор C работает лучше остальных, так как площадь под кривой (AUC) наибольшая.

Ключевым моментом данной работы является сравнение классификаторов, полагаясь на оценку дефекта независимо от пороговых значений, т.е. по всем возможным комбинациям стоимостей ошибочной классификации и априорных вероятностей fp и nfp модулей. Таким образом, для анализа была выбрана метрика ROC-AUC. Преимуществом анализа ROC-AUC является его устойчивость к имбалансным распределениям классов, чем обладают задачи прогнозирования дефектов программного обеспечения. ROC-AUC способен значительно улучшить сходимость эмпирических экспериментов в прогнозировании дефектов программного обеспечения, поскольку он разделяет прогнозируемую производительность и условия эксплуатации. Кроме того, ROC-AUC имеет четкую статистическую интерпретацию: он измеряет вероятность того, что классификатор ранжирует случайно выбранный модуль fp выше, чем случайно выбранный модуль nfp, что эквивалентно тесту Вилкоксона.

Далее определим используемый в дальнейшем статистический подход, называемый пост-фактумным тестом Неймения. Для всех пар классификаторов он сравнивает средние ранги (AR), и объявляет, какие из них «значительно» отличаются друг от друга, то есть превосходят следующаю критическую величину:

Здесь K – количество наборов данных (датасетов); L – количество классификаторов; r_i_j – индивидуальный ранг классификатора i на датасете j; q – табличое значение из диапазона статистики Studentization.

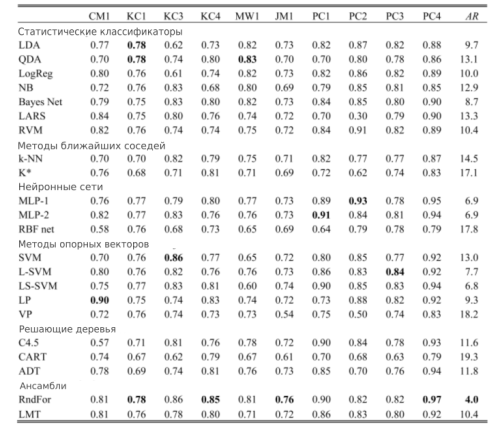
Теперь перейдем к описанию экспериментов. Данные устроены следующим образом: 10 наборов (датасетов) для прогнозирования дефектов программного обеспечения. Каждый датасет состоит из нескольких программных модулей. После препроцессинга модули, содержащие ошибки, обозначаются fp, а не содержащие — nfp. Отдельные атрибуты датасетов и статистики представлены в Таблице 1.

Таблица 1.

В экспериментах рассматриваются 22 классификатора, разделенных на следующие категории: статистические подходы, методы ближайших соседей, нейронные сети, деревья, ансамбли. Стоит также отметить, что некоторые из рассматриваемых классификаторов (SVM, Random Forest, logistic model trees) не нашли широкое применение в прогнозировании дефектов программного обеспечения. Наш выбор руководствуется целью нахождения значимого баланса между широкоприменяемыми методами и новыми подходами. Мы считаем, что наиболее важные представители различных областей (статистика, машинное обучение, глубинное обучение и т.д.) представлены среди классификаторов. Датасеты разделяются на 33% тестовой выборки и 67% обучающей. Метод grid-search с метрикой AUC (т. к. именно она будет использована в дальнейшем) применен для подбора гиперпараметров, которыми обладают большинство классификаторов. Результаты представлены в Таблице 2. выделены значения у классификаторов, достигших наибольшие AUC в опреденных датасетах, а также указаны из средние ранги.

Таблица 2.

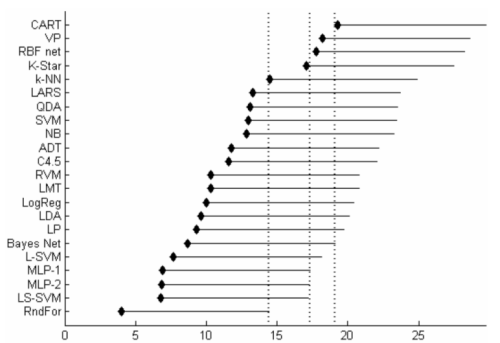
Тем не менее, чтобы оценить классификаторы и определить, какие из них превосходят над другими, необходимо проверить, насколько различия AUC значительны. Это может быть достигнуто с применением описанного ранее пост-фактумного теста Неймения (a = 0.05), то есть проведения парных сравнений между различными классификаторами и проверки, на каких из них разница рангов превышает критическую. Результаты попарного сравнения изображены на Рис. 2. На осях диаграммы отображены классификаторы, упорядоченные в порядке средних рангов, и сами средние ранги. Отрезок справа от каждого классификаторы представляет соответствующую ему критическую разницу. То есть правый конец линии указывает, от какого значения текущее отступает на фиксированную критическую величину (CD). Для лучшей наглядности пороги обозначены пунктирными линиями. Левая линия связана с Random Forest, то есть все классификаторы правее нее работают значительно хуже. Также может быть видно, что значительно хуже Multi-Layer Perseptron работают классификаторы CART, voted preseptron (VP), radial basis function network (RBF net). Аналогично, Bayesian network ограничивает CART. Таким образом, статистическое сравнение показывает интересный вывод: несмотря на примечательные различия AUC среди классификаторов, все методы, кроме нескольких, существенно не отличаются. Следовательно, выбор модели классификации является менее важным этапом в прогнозировании дефектов программного обеспечения, и был переоценен в предыдущих исследованиях.

Рис. 2.

Стоит также отметить, что классификация лишь шаг к достижению наилучшей точности предсказаний. Препроцессинг данных, например, удаление ненужных атрибутов, дискретизация или скейлинг, может значительно улучшить результаты работы классификаторов.

Общим выводом, который можно сделать из эксперимента сравнительного анализа, является то, что показателя эффективности предсказания не хватает, чтобы оценить достоинство модели классификации, и должны быть использованы дополнительные критерии, такие как вычислительная эффективность и простота использования классификатора. С другой стороны, наблюдаемые результаты подтверждают предыдущие выводы относительно эффективности RandomForest в задаче прогнозирования дефектов программного обеспечения и позволяют рекомендовать этот классификатор для будущих экспериментов или практических применений. Он быстро обучаем, требует сравнительно небольшую настройку гиперпараметров и оценивает релевантность отдельных атрибутов кода, обеспечивая таким образом не только точность, но и ясность модели.

В данной работе было представлено сравнение 22 моделей классификации над 10 датасетами из репозитория NASA MPD. ROC-AUC был обоснованно заявлен как основной индикатор точности для сравнения результатов, так как он способен значительно улучшить сходимость эмпирических экспериментов в прогнозировании дефектов программного обеспечения. Другой значительный вклад заключается в том, что в данной работе была использована статистическая проверка - пост-фактумный тест Неймения - которая показала, что модели, за исключением некоторых, показывают результаты точности, незначительно отличающиеся друг от друга. Так как линейные модели (LogReg, LP и LDA) показали аналогичные результаты, что и более сложные, может быть сделан вывод, что данные являются линейно разделимыми. Другими словами, простых классификаторов может быть достаточно, чтобы моделировать связь между статическими атрибутами кода и дефектом программного обеспечения.

Общий уровень точности прогнозирования всех классификаторов подтвердил целесообразность использования классификации для выявления дефектов программных модулей. В частности, предыдущие выводы относительно эффективности RandomForest для прогнозирования дефектов были подтверждены.

Подходящие модели помогают улучшить понимание сбоев в программном обеспечении и их источников, что, в свою очередь, может способствовать развитию новых методов в решении задачи прогнозирования дефектов и предрасположенностей к неисправностям. Кроме того, разработка новых метрик программного обеспечения является перспективной областью для будущих исследований и имеет потенциал для достижения улучшений точности во всех типах классификаторов. Мы надеемся, что предложенная в работе система имеет ценные указания для оценки потенциала соответствующих достижений. Также выводы, полученные в данной работе, могут быть использованы в будующих исследованиях, например, с целью разработки системы оценки многомерного классификатора.

Приложение. Краткие обозначения классификаторов.

1. Статистические классификаторы:

• Linear Discriminant analysis (LDA)
• Quadratic Discriminant analysis (QDA)
• Logistic Regression (LogReg)
• Naive Bayes (NB)
• Bayesian Networks (BayesNet)
• Least-Angle Regression (LARS)
• Relevance Vector Machine (RVM)

2. Методы ближайших соседей:

• k-nearest neighbour (k-NN)
• K-Star (k*)

3. Нейронные сети:

• Multi-layer Perseptron (MLP)
• Radial Basis Function Networks (RBF net)

4. Методы, основанные на опорных векторах:

• Support Vector Machine (SVM)
• Lagrangian SVM (L-SVM)
• Least Squares SVM (LS-SVM)
• Linear Programming (LP)
• Voted Perceptron (VP)

5. Решающие деревья:

• C4.5 Decision Tree (C4.5)
• Classification and regression tree (CART)
• Alternating decision tree (ADT)

6. Ансамбли:

• Random Forest (RndFor)
• Logistic Model Tree (LMT)