Combining Related Products into Product Lines
Оригинал: Julia Rubin, Marsha Chechik, 2012
http://www.cs.toronto.edu/~chechik/pubs/fase12.pdf
Введение
Множество компаний разрабатывает и придумывает целые семейства, связанных между собой продуктов ПО. У этих продуктов схожий набор фич и они удовлетворяют определенным нуждам потребителей. Такие семейства называются software product lines(SPLs). Software Product Line Engineering(SPLE) - это инженерия, направленная на предоставление методов для работы с разработкой SPL. Методы SPLE делятся на 2 категории: композиционные, которые реализуют функции продукта в качестве отдельных фрагментов и позволяют генерировать конкретный продукт, составленный из фрагментов, и аннотативные, которые предполагают, что существует один “максимальный” продукт, в котором аннотации указывают на функцию продукта, которую реализует отдельный фрагмент. Далее будет рассматриваться аннотативный подход. Техника повторного использования линейки программных продуктов предлагает забрасывать существующие продукты для создания новых, что кажется очень непрактичным. Наш подход основан на сравнении элементов существующих продуктов друг с другом (путем вычисления взвешенного подобия их соответствующих подэлементов), соответствии тех, чье сходство выше заданного порогового значения, и их слиянии.
Подготовительные мероприятия
Определение 1 (Элемент модели)
Элемент m модели - это кортеж ‹m|id, m|t, m|r, m|v, m|s›, где m|id - это числовой номер элемента, m|t ∈ T - это тип элемента, m|r ∈ R - это роль элемента, m|v - это значение элемента, m|s - это список подэлементов.
Определение 2 (Эквивалентность)
Пусть M1, M2 ∈ 2M отдельные наборы элементов. m1 ∈ M1, m2 ∈ M2 эквивалентны, m1≅m2, если m1|t = m2|t, m1|r = m2|r,
m1|v = m2|v,
m1|s = m2|s. m1=m2, если m1≅m2 и соответствующие деревья подэлементов изоморфны.
Определение 3 (Модель и эквивалентность моделей)
Множество элементов M ∈ 2M является моделью, если все элементы в М связаны в дерево структуры при помощи отношений подэлементов и у любого m ∈ M свой уникальный номер. Модели эквивалентны, M1=M2, если их соответствующие корневые элементы эквивалентны.
Определение 4 (Модель фич и конфигурации)
Пусть задано множество фич элементов F, модель фич FM = ‹F, φ› - это множество фич F ∈ 2F и функция φ, определенная на фичах из F. Конфигурация фич FM - это множество выбранных фич из F, для которых φ(f) = true, f ∈ FM.
Определение 5 (Линейка продуктов)
Линейка продуктов PL = ‹FM, M, R› - это тройка, где FM - это модель фич, M ∈ 2M модель предметной области и R ⊆ F × M - это множество отношений, которые сопоставляют элементам из M фичи из F.
Определение 6 (Выведение продукта)
Пусть PL = ‹FM, M, R› линейка продуктов и пусть FM ее конфигурация фич. Множество элементов M выведено из линейки продуктов PL при конфигурации FM, М = Δ(PL, FM), если:
- для любого m ∈ M, Δ(m) ∈ M ⇔ существует f ∈ FM⋅(f,m) ∈ R.
- для любого m ∈ M существует единственный m ∈ М⋅m = Δ(m).
- для любого m ∈ M существует единственный m ∈ M⋅m = Δ(m).
- m = Δ(m) ⇒ m ≅ m.
- для любого m ∈ M, mc ∈ m|s ⇔ Δ-1(mc) ∈ Δ-1(m)|s ∧ f ∈ FM⋅(f, Δ-1(mc)) ∈ R.
Лемма 1 (Уникальность)
Пусть PL = ‹FM, M, R› линейка продуктов, FM конфигурация фич и M' = Δ(PL, FM). Тогда для каждого M' выполнено M' = M.
Объединение моделей
Определение 7 (Сравнение)
Пусть M1, M2 ∈ 2M - это модели. Сравнение(M1, M2, W) это функция, которая создает тройки C ⊆ (M1 × M2 × [0..1]), которая удовлетворяет следующим пунктам:
- (m1 = m2) ⇒ (m1, m2, 1) ∈ С.
- (m1|t ≠ m2|t) ∨ (m1|r ≠ m2|r) ⇒ (m1, m2, 0) ∈ С.
- m1|t = m2|t = Ref ⇒ (m1, m2, x) ∈ С ⇔ (M1[m1|v], M2[m2|v], x) ∈ C
m1|t = Ref ∧ m2|t ≠ Ref ⇒ (m1, m2, x) ∈ С ⇔ (M1[m1|v], M2[m2], x) ∈ C
m1|t ≠ Ref ∧ m2|t = Ref ⇒ (m1, m2, x) ∈ С ⇔ (M1[m1], M2[m2|v], x) ∈ C. - m1|t = m2|t = T, m1|r = m2|r = R, T атомное ⇒ (m1, m2, 1) ∈ С ⇔ x = compareT,R(m1, m2).
Определение 8 (Сопоставление)
Пусть M1, M2 ∈ 2M - это модели и пусть С - это множество троек, порожденных сравнением (M1, M2, W). Тогда сопоставление(M1, M2, С, S) - это функция, которая создает наборы пар S ⊆ (M1 × M2), для которой выполняется следующее:
- (m1, m2) ∈ S ⇒ для любого (m1', m2') ∈ S(m1'|id = m1|id ⇔ m2'|id = m2|id).
- m1|t = m2|t = T, T атомное ⇒ (m1, m2) ∈ S ⇔ (m1, m2, 1) ∈ С.
- m1|t = m2|t = T, T составное ⇒ (m1, m2) ∈ S ⇔ (m1, m2, x) ∈ С ∧ x ≥ ST.
Определение 9 (Слияние)
Пусть M1, M2 ∈ 2M - это модели и пусть С - это множество троек, порожденных сравнением (M1, M2, W) и сопоставлением(M1, M2, С, S). Тогда слияние(M1, M2, S) - это функция, которая создает слившуюся модель M, которая удовлетворяет следующим свойствам:
- (m1, m2) ∈ S ⇔ σ(m1)=σ(m2).
- для любого m1 ∈ M1 существует единственный m ∈ M⋅m = σ(m1) и для любого m2 ∈ M2 существует единственный m ∈ M⋅m = σ(m2).
- для любого m ∈ M⋅(существует единственный m1 ∈ М1⋅m1 = σ1-1(m))∨(существует единственный m2 ∈ М2⋅m2 = σ2-1(m)).
- для любого m ∈ М1 U М2, для любого m ∈ M, m = σ(m) ⇒ m ≅ m.
Рефакторинг продуктовой линейки
Определение 10 (Слияние в процессе построения)
PL' = ‹FM', M', R'› линейка продуктов, построенная слиянием продукта M в продуктовую линию PL(PL' = PL⊕W,SM, используя следующие правила:
- если FM = ‹F, φ›, тогда FM' = ‹F', φ'›, F' = F U {fM|fM∈F, fM ∉ F} и φ' = (φ ∨ fM) ∧ ‾(fM∧f).
- если C = сравнение(M, M, W) и S = сопоставление(M, M, C, S), тогда M' = слияние(M, M, S).
- R' = {(f, σ(m))| f ∈ F, m ∈ M, (f, m) ∈ R} U {(fM, σ(m))}| m ∈ M}.
PL - это первоначальная продуктовая линейка, PL' - это конечная продуктовая линейка.
Корректность рефакторинга продуктовой линейки
Лемма 2
Пусть FM - это подмножество FM. Тогда FM - это конфигурация фич FM ⇔ - это конфигурация фич FM'.
Лемма 3
Пусть FM - это подмножество FM. Если FM - это конфигурация фич FM , M = Δ(PL, FM) и M' = Δ(PL', FM), тогда M = M'.
Ниже приведено схематичное доказательство Леммы 3:
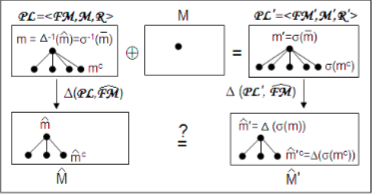
Лемма 4
{fM} - это конфигурация фич PL'.
Лемма 5
Пусть {fM} - это конфигурация фич. Тогда модель, полученная из PL' c этой конфигурацией, эквивалентна М. М = Δ(PL', {fM}).
Теорема 1
[PL'] = [PL] U {M}.
Заключение
В этой работе была формально определена простая информационная модель и техники рефакторинга для трансформированная отдельных продуктов в более компактное представление продуктовой линейки.