Изложение статьи
Yuming Zhou and Hareton Leung,Empirical analysis of object-oriented design metrics for predicting high and low severity faults, IEEE TRANSACTIONS ON SOFTWARE ENGINEERING, VOL. 32, NO. 10, OCTOBER 2006
Введение
В статье рассматривается задача выявления дефектов (определение вероятности того, что в классе содержится дефект архитектурного решения). Для решения данной задачи используются метрики Чидамбера и Кемерера(было выбрано 6 метрик), которые оценивают структурные характеристики классов. Для исследования используются четыре различных метода машинного обучения:
- Логистическая регрессия
- Наивный байесовский классификатор
- Случайный лес
- Метод ближайшего соседа
В статье рассматриваются следующие вопросы:
1. Как метрики, связанны с возникновением ошибок высокой и низкой сложности в классах?
2. Какие метрики сильнее связаны с возникновением ошибок высокой и низкой сложности в классах?
3. Насколько точно метрики предсказывают ошибки высокой степени тяжести?
4. Насколько точно метрики предсказывают ошибки низкой степени тяжести?
Используемые метрики и датасеты
В статье рассматриваются следующие метрики:
- Weighted Methods per Class (WMC) - количество методов, имплементируемым классом
- Depth of Inheritance (DIT) - расстояние от класса до корня в дереве насследования
- Response for a Class (RFC) - WMC плюс количество наследованных методов
- Number of Children (NOC) - число непосредственных детей в дереве насследования у данного класса
- Coupling between Objects (CBO) - количество классов, с которым связан данный класс (fan-out)
- Lack of Cohesion (LCOM) - усредненная по атрибутам доля методов, использующая этот атрибут (LCOM3)
- Source Lines Of Code (SLOC) - количество строк кода в классе
Для каждой метрики проверяется следующая гипотеза: У класса с высоким значением метрики больше шансов иметь ошибку высокой/ низкой сложности, чем у класса с низким значением метрики.
В качестве выборки используется датасет KC1 (NASA), в котором даны измерения по 21 метрике для классов и методов. Для анализа используются только 7 вышеперечисленных метрик. Из него были удалены все случаи не связанные с ошибками в исходном коде. Так же все дефекты были разделены на две группы(ошибки высокой и низкой сложности), вместо 5-ти исходных.
Вычислительный эксперимент
В рамках вычислительного эксперимента для каждой из моделей оцениваются такие параметры, как полнота (доля отмеченных классов как дефект от общего числа дефективных классов)(Correctness), точность (доля правильно отмеченных дефектов) (Precision), и доля правильно данных предсказаний (Completeness).
Методика эксперимента следующая: для каждой модели проводятся измерения на трёх датасетах:
- С любыми дефектами(Ungraded severity faults)
- Только дефекты высокой сложности(High severity faults)
- Только дефекты низкой сложности(Low severity faults)
и измеряются необходимые характеристики.
Вначале была построена модель логистической регрессии с использованием одной метрики(т.е. изучались связи отдельных метрик с возникновением ошибок). Далее были построены модели для анализа зависимости от комбинации метрик проектирования(все кроме SLOC) и всех метрик с использованием различных методов машинного обучения.
Результаты измерений
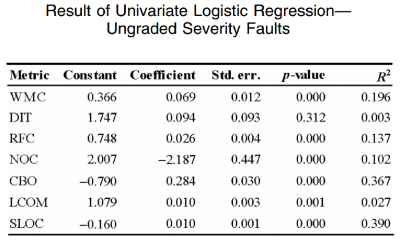
Логистическая регрессия для отдельных метрик
 Логистическая регрессия для комбинаций метрик
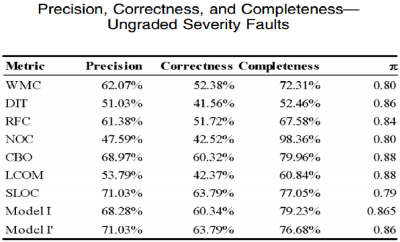
Логистическая регрессия для комбинаций метрик
 Методы ML для отдельных метрик и их комбинаций
Методы ML для отдельных метрик и их комбинаций
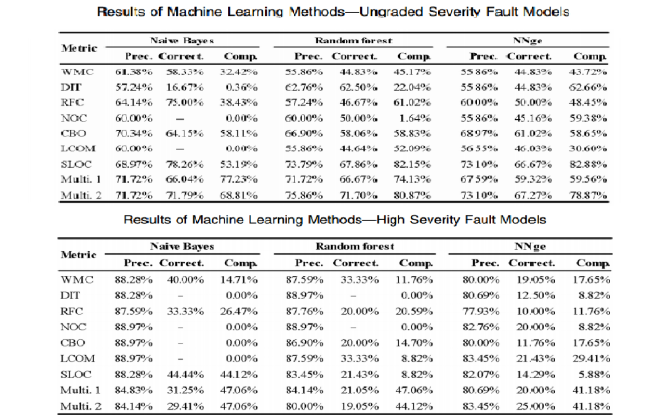
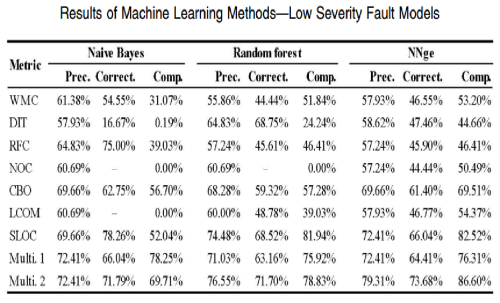
Можно заметить, что для ошибок высокой сложности, как одномерные так и многомерные модели логической регрессии имеют достаточно низкую корректность и полноту, хотя они и имеют высокую точность. В частности, из всех метрик, SLOC является лучшим предсказателем. Многомерная модель построенная только с метриками проектирования не опережает даже простую модель, с зависимостью от размера класса. Точность, корректность и полнота моделей машинного обучения также хуже, чем у регрессионной модели. Эти результаты указывают на то, что возможности этих метрик проектирования для предсказания ошибок высокой сложности ограничены, хотя большинство из них статистически связаны с возникновением дефектов высокой сложности.Точность, корректность и полнота для моделей машинного обучения более или менее равны таковым в модели логистической регрессии. Эти результаты свидетельствуют о том, что метрики проектирования работают намного лучше в прогнозировании неисправностей низкой сложности, чем при прогнозировании неисправностей высокой сложности.
В итоге используя результаты измерений, были проверены сформированные в начале эксперимента гипотезы.
Результаты проверки гипотез
Заключение
Основные полученные результаты:
- Метрики CBO, WMC, RFC и LCOM статистически связаны со склонностью кода к дефектам любой сложности, в то время как DIT не связан с возникновением дефектов. Величина NOC связана с количеством дефектов низкой степени сложности обратной зависимостью(класс с большим значением NOC имеет меньшую вероятность быть дефектным)
- Возможности прогнозирования склонности к дефектам этих метрик сильно отличаются в зависимости от серьезности дефекта. Применительно к классификации классов на подверженные и не подверженные ошибкам для ошибок низкой сложности, модели логистической регрессии и машинного обучения смогли достичь показателей производительности, сравнимых с предыдущими исследованиями. Однако, возможности предсказаний с помощью этих показателей для ошибок высокой сложности ограничено.
