Martin Hitz and Behzad Montazeri. 1996. Chidamber and Kemerer's Metrics Suite: A Measurement Theory Perspective. IEEE Trans. Softw. Eng. 22, 4 (April 1996), 267-271. DOI=http://dx.doi.org/10.1109/32.491650

Набор метрик для оценки систем, построенных на принципах ООП, продвигаемый Chidamber-ом и Kemerer-ом оценивается с точки зрения теории метрик. На примере метрики зацепленности классов (Coupling between Object Classes) показано, что плохая эмпирическая система связей может привести к недостаткам в метриках ПО. Таким же образом, для метрики связности (точнее, обратной ей) Lack of Cohesion in Methods показано, что репрезентативность метрики должна проверяться, даже если остальные принципы соблюдены. Дополнительно предложена альтернативная версия метрики LCOM.

Chidamber и Kemerer в своей статье предожили набор метрик для оценки систем, построенных на принципах ООП. В своей более поздней статье они провели более тщательный анализ предложенных метрик и предложили ряд рекомендаций по их использованию. Но если исследовать эти метрики внимательнее, то можно заметить ряд недостатков, которых можно избежать, если применить простые принципы теории метрик. В этой статье с применением теории метрик показываются сильные и слабые стороны предложенных Chidamber-ом и Kemerer-ом метрик на примере CBO и LCOM.

Перед тем, как что-то измерить, нам нужен объект, к которому применять метрику. Причем этот атрибут должен иметь некоторую важность по отношению к ПО, которое мы рассматриваем. Также этот объект может быть не важен сам по себе, но может являться некоторой переменной в метрике для другого “важного” объекта. Следующим шагом будет определение эмпирической системы связей, которая включает в себя все общие интуитивные идеи о рассматриваемом объекте. Далее на примере метрики CBO показывается, какие последствия влекут отклонения от этого правила. Рассмотрим метрику Coupling Between Object Classes. Она определена как сумма 2-х величин: количества классов, методы и атрибуты которых данный класс использует в своих методах, и количества классов, которые используют методы и атрибуты данного класса в своих методах. Но для более полной эмпирической системы связей необходимо учесть, что разные классы могут давать разный вклад в метрику в зависимости от ситуации. Например можно рассмотреть следующие эмпирические связи:

• обращение к атрибутам объекта влечет более сильную зацепленность, чем обращение к методам
• обращение к атрибутам классов-родителей влечет меньшую зацепленность, чем обращение к атрибутам других классов
• нарушение закона Деметры влечет большую зацепленность, чем отсутствие нарушения.

Рассмотрим пример:

// Example 1
class A { ... void g(); ...};
class B { ... A* f(); ... };
class C {
    A* a;
    B* b;
    void M () { a->g(); b->f()->g();};
}
// Example 2
class A { ... void g(); ...};
class B { ... A* f(); void apply_g(); ... };
class C {
    A* a;
    B* b;
    void M () { a->g(); b->apply_g(); }
};

В рассмотренном выше примере CBO(C)=2 в обоих случаях, хотя в первом примере происходит нарушение закона Деметры, а в правом нет. Таким образом, важно определить систему эмпирических связей (то есть те связи между объектами, которые мы будем рассматривать) прежде чем считать метрики. И так же важно, чтобы посчитанные метрики удовлетворяли нашей выбранной системе связей.

После того, как была определена система эмпирических связей, метрика M должна удовлетворять некоторой эмпирической связи R между объектами следующим образом: <latex> xRy \leftrightarrow M(x) < M(y)</latex>. Это условие называется условием репрезентативности, а задача валидации метрики ПО - это проверка этого условия. Валидация метрики может сопровождаться другими соображениями, но не может быть полностью ими заменена. Рассмотрим как пример метрику Cohesion - мера взаимосвязи между элементами одного модуля ( в ООП обычно рассматривается класс), степень связи между задачами, выполняемыми элементами модуля. Для определения этой метрики нужно учесть много семантической информации, что нельзя сделать автоматически. C&K решая эту проблему вводят метрику, обратную Cohesion - Lack of Cohesion in Methods, которая равна разности количества пар методов, использующих непересекающиеся множества атрибутов, и количества пар методов, использующие множества атрибутов, пересекающиеся хотя бы по одному элементу. Но такое определение имеет некоторые аномалии по отношению к интуитивному восприятию связности. Рассмотрим пример (методы класса - овалы, точки - поля класса, которые они используют):

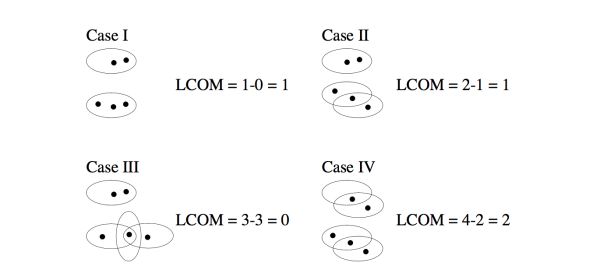
В нашем интуитивном понимании связности, все приведенные классы должны быть разбиты на 2, хотя значения LCOM разные. Сложно объяснить, почему добавление метода в существующий кластер в 1 случае не изменяет степень связности во втором, притом, что проделывая такую же операцию в случае 2 мы получаем противоречивые результаты: в случае 3 LCOM уменьшается, а в случае 4 увеличивается. Таким образом, предлагается вместо этой LCOM использовать LCOM, определенную как количество кластеров методов, которые обращаются к одинаковым атрибутам класса. Можно переформулировать это в терминах теории графов. Рассмотрим граф G, в котором множество вершин это методы класса, а ребро между двумя методами проводится тогда и только тогда, когда они обращаются хотя бы к одному общему полю класса. Тогда мы можем определить LCOM как количество связных компонент в полученном графе, что полностью эквивалентно формулировке через кластеры. Но в случае LCOM = 1 все равно есть более или менее связные классы, тогда можно уточнить LCOM принимая во внимание количество ребер в графе G. То есть если LCOM = 1 и количество ребер = n - 1, где n - количество вершин, то это случай минимальной связности, а если LCOM = 1 и количество ребер <latex> \frac{n(n - 1)}{2} </latex>(полный граф), то это случай максимальной связности. Для удобства можно перевести все в интервал [0, 1].

Аномалии LCOM, рассмотренные выше, не были замечены C&K частично потому, что валидация условия репрезентативности была заменена другим набором правил (аксиомами Weyuker). Но любой такой набор правил может быть использован только в дополнение к более фундаментальному условию репрезентативности. Также, касательно применения аксиом Weyuker, есть несколько проблем: в своей работе она использует видение программ как объектов, состоящих из более мелких программ, что не совсем применимо к ООП, поскольку тут мы основываемся на классах, как составляющих. Также, существует несколько методов получения класса AB из классов A и B: сделать класс, который содержит A и B как подобъекты, сделать этот класс, наследуя B от A или сделать новый класс, наследуясь одновременно от A и B. В любом случае, при валидации тогда нужно рассматривать все способы такого образования класса AB.

В статье было показано, что метрики, предложенные C&K могут быть улучшены, если следовать некоторым принципам теории метрик. Также был показан способ построения метрики, которая будет отвечать нужным требованиям. Этот способ также можно использовать для анализа уже существующих метрик, как было показано на примере CBO и LCOM.

1. Оригинальная статья: http://people.dsv.su.se/~joco2917/hitz96chidamber16.pdf